编辑:无损检测证书挂靠 时间:2025-02-11 11:06:17
包扬(1989-),男,讲师,研究方向为涡流无损检测
无损检测是指在不破坏检测目标的情况下检测出其中的缺陷以及材料的不连续性,是一项典型的具有低投入、高产出特点的工程应用技术[1]。电磁无损检测技术广泛应用于核电站、高速铁路、特种设备等检测领域[2-4]。脉冲涡流检测技术属于电磁无损检测技术中的一种,通过在激励线圈中输入脉冲电流,进而在被测物体的近表面激发出涡流,而涡流又反作用于激励线圈,通过测量激励线圈的电压、电阻等信息可获得被测物体有无缺陷以及实现对其材料的表征[5-7]。脉冲涡流无损检测技术成本低且检测速度快,非常适合于金属物体内部缺陷的定量检测[8]。
涡流无损检测系统均有一定的检测误差及不确定性,这会影响缺陷的探测概率(Probability of detection, PoD)[9]。探测概率的研究对于量化无损检测系统对缺陷的探测能力以及系统的可靠性十分重要[10-11]。然而,探测概率的研究需要大量的试验数据用以确定回归模型的参数,模型辅助探测概率方法使用与基准试验算例相验证的物理模型获得所需要的数据,提升了探测概率问题的研究效率[12]。
许多高效的物理模型都被用于涡流无损检测问题的仿真。其中基于有限元法的物理模型因其相较于边界元法(Boundary element method, BEM)更容易应用于不同问题的求解而获得广泛关注,然而其需要对整个求解空间进行离散故而需要大量的计算资源。在边界元法中,只需要对探测物体表面进行离散,虽然边界元法有平方阶的阻抗矩阵存储和迭代求解运算的缺点,但是该问题可以通过使用快速算法来解决[13-17]。
考虑到检测系统中高不确定性导致的多随机变量需要产生大量模型响应的情况,仅仅依靠高效的物理模型仍然很难达到模型辅助探测概率研究所需的效率要求,因此元模型(Metamodel)应运而生。元模型是一种高效的计算模型,可以用来代替精确但是计算耗时的物理模型,也被应用在无损检测领域[18-19]。MIORELLI等[20]使用支持向量回归法对涡流无损检测和超声检测问题构建了元模型。BROWNE使用克莱金法构建元模型应用于模型辅助探测概率的求解。DU等[21]将多项式混沌展开法应用到超声波检测中。PERSSON等[22]对超声检测使用表面响应元模型辅助探测概率的研究。但是上述工作使用的是有限元法或解析法,并没有使用高效近线性阶的基于快速算法加速的边界元法,此外,也没有使用基于多项式混沌展开法的元模型对三维涡流无损检测问题的探测概率进行研究。
文章首先介绍了基于退化核函数加速的边界元法的三维涡流无损检测问题的数值模型,然后提出使用基于普通最小二乘法(Ordinary least squares, OLS)的多项式混沌展开法(Polynomial chaos expansion, PCE)的元模型提升涡流无损检测问题探测概率的效率。该元模型对于训练点和预测点分别选取拉丁超立方法和蒙特卡洛法,使用与随机变量概率密度函数相正交的多项式基函数对随机变量进行谱表示,通过普通最小二乘法求解基函数的系数。最后,通过有限截面线圈检测金属板面槽的算例,引入线圈位置和提离距离为不确定传播的参数,测试所提出元模型的求解精度和效率。测试结果表明,该元模型预测的模型参数与基于退化核函数加速的边界元法物理模型计算的模型参数相对误差在1 %以内,极大降低了所需的计算开销。
在边界元法中,使用无低频崩溃问题的Stratton-Chu方程对三维涡流无损检测问题建模[23]
| (1) |
| (2) |
式中:Einc和Hinc为入射电磁场;S为所感兴趣区域的边界;r和r′∈S,分别为场点和源点;ω为角速度;μ0和ε为真空中磁导率和介电常数;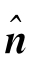 为指向求解域的单位法向量;G(r,r′)=e-jk|r-r′|/(4π|r-r′|),为积分方程的核函数;
为指向求解域的单位法向量;G(r,r′)=e-jk|r-r′|/(4π|r-r′|),为积分方程的核函数;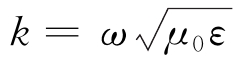 为波数。
为波数。
在边界元法中,使用RWG基函数展开等效面电、磁流,用脉冲基函数展开磁场的法向分量,测试方法选用伽辽金法,得到的阻抗矩阵为
| (3) |
式中:算子的下标l=1,2,分别代表空气和金属媒质;上标×和n分别代表与单位法向量的叉乘和点乘;T和D为对角矩阵;K和L为磁(电)流产生的电(磁)场;R为电(磁)荷产生的电(磁)场。
使用八叉树结构对目标进行分块,根据场区块和源区块之间距离的关系,将其分为近区块和远区块。其中近区块表示场区块和源区块重合或是邻近,其余的为远区块。对于具有秩亏特性的远区块v=t×s,其中t和s分别为场区块和源区块,对核函数及其梯度使用拉格朗日多项式将其插值退化为
| (4) |
| (5) |
式中:K={1,2,…,p}d;d=1, 2, 3,分别对应1维,2维,3维问题;p为每个维度中插值点的个数;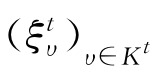 和
和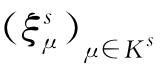 分别为场区块和源区块中的插值点;Kt和Ks分别为场、源区块中的插值点个数;
分别为场区块和源区块中的插值点;Kt和Ks分别为场、源区块中的插值点个数;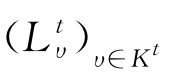 和
和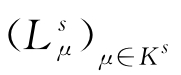 为相应的拉格朗日插值多项式。
为相应的拉格朗日插值多项式。
对阻抗矩阵进行核函数退化,首先考虑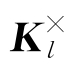 子矩阵的远区块,假设其维度为T×Q,则有
子矩阵的远区块,假设其维度为T×Q,则有
| (6) |
式中:Λ(r)为RWG基函数。
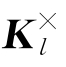 子矩阵可以近似为
子矩阵可以近似为
| (7) |
因为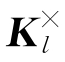 子矩阵远区块的秩远小于T和Q的值,所以通过退化核函数方法降低了该矩阵的存储量。退化核函数的方法也可以应用到其他子矩阵中,从而构建高效且精确的近线性阶的涡流无损检测数值模型。文章中使用退化核函数加速的边界元法物理模型(KD-BEM)对模型辅助探测概率问题进行分析。
子矩阵远区块的秩远小于T和Q的值,所以通过退化核函数方法降低了该矩阵的存储量。退化核函数的方法也可以应用到其他子矩阵中,从而构建高效且精确的近线性阶的涡流无损检测数值模型。文章中使用退化核函数加速的边界元法物理模型(KD-BEM)对模型辅助探测概率问题进行分析。
多项式混沌展开法由Wiener提出,是一种可以有效描述随机过程不确定性传播的元模型[24-25]。考虑定性映射表示的物理模型响应y=M(x),其中矢量x={x1,…,xn}T∈Rn,n≥1为输入变量,矢量y={y1,…,yQ}T∈RQ,Q≥1为物理模型响应。由于输入矢量x有不确定性的影响,使用规定概率密度函数的独立随机矢量X表示。因此,模型响应也使用随机变量表示为Y=M(X)。使用正交的多项式基函数将Y展开
| (8) |
式中:ψi为多元多项式基函数;i为多项式项的索引;ai为与基函数相应的未知系数。
实际中,使用有限阶数的多项式基函数就可以达到求解的精度要求,因此将多项式截断
| (9) |
式中:MPC(X)为截断近似后的多项式混沌展开模型。
所需多项式的项数P为
| (10) |
式中:p为多项式混沌展开模型的阶数;n为随机变量的个数。
将物理模型计算出的观察点的真实响应值,用多项式混沌展开法对相同观察点的预测值和相应的残差表示为
| (11) |
式中:εPC为残差。
使用普通最小二乘法来求解多项式混沌展开法的系数降低残差,求解出的系数为
| (12) |
式中:Ai,j=ψi(xj),j=1,…,n,i=1,…,P。
通过计算均方根误差以及归一化的均方根误差来验证所求得的多项式混沌展开模型的精度,均方根误差的计算式为
| (13) |
式中:Nt为总的训练点个数;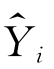 和Yi分别为第i个训练点的元模型预测值和模型的实际响应值,归一化均方根误差为均方根误差除以模型响应Yi的范围,即响应最大值减去响应最小值。
和Yi分别为第i个训练点的元模型预测值和模型的实际响应值,归一化均方根误差为均方根误差除以模型响应Yi的范围,即响应最大值减去响应最小值。
构建多项式混沌展开元模型的步骤如图1所示。首先,通过拉丁超立方法选取任意数量的训练点,使用基于退化核函数加速的边界元数值模型计算训练点的实际响应值,使用响应值计算未知系数从而获得模型;然后,使用蒙特卡洛法(Monte Carlo Sampling,MCS)生成预测点,使用数值模型计算预测点的实际响应值,比较实际响应值和通过多项式混沌展开模型计算出的预测响应值;最后,如果所求元模型的均方根误差和归一化的均方根误差小于所设阈值,那么计算出的多项式混沌展开模型就满足精度要求,否则需要增加训练点的个数直到模型满足精度要求为止。
探测概率曲线表示特定缺陷尺寸的探测概率,通过构建“â-a”回归曲线来分析。探测概率的计算式为
| (14) |
式中:Φ为正态累积分布函数;μ和σ分别为均值和标准差。
对数坐标系中的均值μ和标准差σ分别为
| (15) |
| (16) |
式中:β0, β1和σr可以由最大似然法求得[26]。
通过有限截面线圈检测金属板面槽的算例测试所提出的多项式混沌展开法元模型的精度和效率,元模型所需计算开销依赖于所需的训练点对应的物理模型响应。在有限截面线圈检测金属板面槽(见图2)的问题中,检测线圈的内径为9.34 mm,外径为18.40 mm,线圈匝数为408,金属板厚度为12.22 mm,电导率为30.6 MS/m,面槽深度为5.00 mm,宽度为0.28 mm,长度为0.1~0.5 mm,间隔为0.1 mm。工作频率为7 000 Hz,探测线圈x、y轴的位置和提离距离l为不确定传播参数,其经验分布如表1所示。
| 参数 | 算例1 | 算例2 |
|---|---|---|
| 提离距离l | N(2, 0.5) | N(2, 1) |
| x轴位置 | N (13, 0.5) | U (12, 14) |
| y轴位置 | N (0, 0.5) | U (-1, 1) |
在算例1中,提离距离l、线圈x轴、y轴的位置均为正态分布,使用MCS法对每个面槽长度选取1 000个预测点,共需要使用KD-BEM物理模型计算5 000个预测点的模型响应值作为基准。为了使每个面槽长度对应的元模型预测的响应相较于纯物理模型的基准响应的归一化均方根值达到小于1 %的精度要求,多项式混沌展开(OLS-PCE)元模型在每个面槽长度所需的训练点个数为500个,总共需要计算2 500个训练点的数值模型响应来构建元模型。面槽长度所对应的归一化均方根误差如图3所示,可知,每个面槽长度运行500次物理模型即可以保证构建的元模型的精度要求,多项式混沌展开模型所需的计算开销是纯KD-BEM物理模型的50 %。
使用多项式混沌展开法构建的元模型对探测概率进行研究,得到的探测概率指标如表2所示,其中使用5 000个预测点的纯KD-BEM物理模型得到的回归参数与使用多项式混沌展开模型对2 500个训练点预测得到的回归参数 μ和σ分别为-0.553 5 mm和0.103 6 mm,a50和a90分别为0.574 9 mm和0.656 5 mm,而多项式混沌展开模型对2 500个训练点预测得到的回归参数μ和σ分别为-0.554 8 mm和0.104 6 mm,a50和a90分别为0.574 2 mm和0.656 5 mm,相对误差分别为0.23 %,0.97 %,0.13 %和0.001 2 %,均小于1 %。所构建的元模型预测的â-a回归分析和探测概率如图4所示。通过以上分析可知,多项式混沌展开法所构建的元模型可以高效且精确地替代纯物理模型进行辅助探测概率的研究。
| 指标 | KD-BEM物理模型 | OLS-PCE元模型 |
|---|---|---|
| μ | -0.553 5 | -0.554 8 |
| σ | 0.103 6 | 0.104 6 |
| a50 | 0.574 9 | 0.574 2 |
| a90 | 0.656 5 | 0.656 5 |
在算例2中,提离距离l为正态分布,而线圈x轴、y轴的位置符合均匀分布。使用MCS法对每个面槽长度选取1 000个预测点,共需要使用KD-BEM物理模型计算5 000个预测点的模型响应值作为基准。为了使每个面槽长度对应的元模型预测的响应相较于纯物理模型的基准响应的归一化均方根值达到小于1%的精度要求,在OLS-PCE元模型中,每个面槽长度所需的训练点个数为250个。使用多项式混沌展开法构建的元模型对探测概率进行研究,得到的探测概率指标如表3所示,其中使用5 000个预测点的纯KD-BEM物理模型得到的回归参数μ和σ分别为-0.546 9 mm和0.206 6 mm,a50和a90分别为0.578 7 mm和0.754 2 mm,而多项式混沌展开模型对1 250个训练点预测的回归参数μ和σ分别为-0.550 4 mm和0.205 2 mm,a50和a90分别为0. 576 7 mm和0. 750 1 mm,相对误差分别为0.64 %,0.71 %,0.35 %和0.53 %,均满足精度要求。多项式混沌展开模型所需的计算开销是纯KD-BEM物理模型的25 %。所构建的元模型预测的â-a回归分析和探测概率如图5所示。通过以上分析可知,多项式混沌展开法所构建的元模型又一次高效且精确地替代了纯物理模型。
| 指标 | KD-BEM物理模型 | OLS-PCE元模型 |
|---|---|---|
| μ | -0.546 9 | -0.550 4 |
| σ | 0.206 6 | 0.205 2 |
| a50 | 0.578 7 | 0.576 7 |
| a90 | 0.754 2 | 0.750 1 |
提出一种将基于退化核函数加速的边界元法的数值模型和基于普通最小二乘法的多项式混沌展开算法的元模型相结合,提升三维涡流无损检测问题探测概率效率的方法。测试结果表明在探测概率的研究中,只需要计算较少数量的响应值即可构建元模型,所需的计算开销相较纯物理模型的开销至少节省50 %。该元模型预测的探测概率分析指标与基于退化核函数加速的边界元法物理模型计算的指标相对误差在1 %以内。提出的元模型也可以推广到其他无损检测问题探测概率的分析中,在保证模型指标精度的情况下提升求解效率。
推荐阅读:2025年无损检测证书挂靠价格趋势预测