编辑:无损检测证书挂靠 时间:2025-03-10 21:05:14
作者简介:阮隽宇(2000—),男,硕士研究生,主要研究方向为漏磁检测,1163037899@qq.com
漏磁检测因检测速度快、不需要耦合剂并且可实现在役检测的优势成为了运输管道快速检测的主要手段[1-2]。分析缺陷的漏磁信号特征,确定缺陷尺寸是漏磁检测中的难题[3-4]。目前业内主要基于映射的方法,对管道缺陷的轮廓进行二维重构,从而建立缺陷信号与几何尺寸之间的联系[5-6],缺陷漏磁场的计算多采用数值法,其中有限元分析方法应用最为广泛。LE等[7]基于有限元模拟仿真结果实现了对未知数据的磁场分布的准确预测,WANG等[8]和YOUSAF等[9-10]分别用COMSOL仿真软件构建了缺陷试件和漏磁场模型。目前,已有多位学者利用漏磁检测信号对缺陷进行重构研究分析,FENG等[11]根据漏磁信号的轴向磁通分量,构建神经网络重构缺陷轮廓。KANDROODI等[12]从漏磁信号的测量结果中提出了推导缺陷位置和估算缺陷宽度的新方法。PENG等[13]在研究漏磁信号特征的基础上,实现了腐蚀缺陷量化与预测。DAI等[14]认为缺陷的漏磁检测结果受缺陷尺寸和位置以及缺陷形状等因素的影响。ZHEN等[15]分析了管道变形临界参数(高度、长度、倾斜角)与漏磁信号之间的关系,将信号特征量代入计算模型后实现了较高精度的缺陷尺寸求解。上述分析方法都建立在分析漏磁信号以及提取其特征的基础上,均着眼于对缺陷的长度和深度进行量化,而依然难以准确描述缺陷特征。
文章利用COMSOL有限元仿真软件,对不同尺寸的缺陷建立了以均匀多匝线圈的直流输入为激励源的仿真模型,通过改变缺陷长度、深度、二维边缘轮廓面积得到不同缺陷励磁后的信号波形和数据,再使用最小二乘曲线拟合方法进行拟合,建立缺陷尺寸和漏磁信号之间的数学关系,并进行了试验验证分析。
数值模拟法利用电磁场的麦克斯韦方程进行求解,而有限元法作为数值解析法的一种,可以将不同几何形状的缺陷整体划分成细小单元求解,在计算漏磁信号时对整个磁场进行剖分计算,漏磁场的麦克斯韦方程为
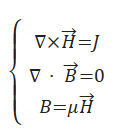
式中:H为磁场强度矢量;B为磁通密度矢量;
假设各点材料的磁导率μ一致。由于磁场的无源性,引入中间量矢量磁位A辅助描述有电流存在时的漏磁场计算问题,可表示为

管道检测产生的磁场可以看作几何结构对称试件的磁场,将直角坐标系转换为(γ,θ,z)的圆柱坐标系,对矢量A求二次梯度的方程式可以化简为
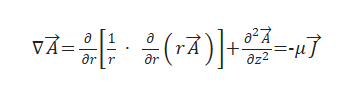
式(5)满足泊松方程,将该方程与电磁场的边界条件结合起来,即可等价为边值问题。COMSOL多物理场仿真软件在计算漏磁场前对构建的几何缺陷进行预处理,通过运行计算可以解得漏磁场磁通密度模以及磁力线在空间中的分布情况。
漏磁检测模型的磁路结构如图1所示,该模型主要由励磁线圈、铁芯和模拟管道检测的试件组成。根据磁场的折射和扩散特性,缺陷附近会产生漏磁场,缺陷参数改变会产生不同幅值及形状的漏磁信号。文章通过有限元仿真模拟获取试件上的漏磁信号,利用COMSOL软件搭建二维仿真缺陷模型,完成模型尺寸设计后,需选择各部分模型的材料。励磁线圈设置为均匀多匝的铜线,线圈电流为5 A,匝数设置为450匝,铁芯选用磁导率较高的软磁材料DT4,管道材料选择Q235,其磁通密度-磁场强度曲线如图2所示。空气模型的相对磁导率μ为1.0。
不同缺陷参数会产生不同的漏磁信号分布,缺陷沿励磁方向的长度、深度以及二维边缘轮廓面积,均影响缺陷漏磁场的分布。即,随着缺陷参数的变化,产生的漏磁信号幅值和形状以及漏磁信号分布情况也会随之改变,因此缺陷参数与漏磁信号特征值之间存在一定的联系。
矩形缺陷是检测过程中最常见的一种缺陷,缺陷深度固定为管道试件厚度的50%,长度分别为1,2,3,4,5,6 mm(缺陷编号分别为1,2,3,4,5,6),在缺陷上方1 mm处设置二维截线,进行模拟检测(取1 mm的提离值),以此截线上的磁通密度(磁感应强度)大小作为传感器输出的漏磁信号,计算得出不同长度缺陷的漏磁信号曲线如图3所示。
由图3可知,当缺陷深度尺寸固定,缺陷的长度逐渐增加时,轴向磁通分量的信号波形宽度逐渐变大,信号中心发生“塌陷”,信号峰值逐渐降低;径向磁通分量的峰值间距不断变大且变化非常明显,因此径向磁通分量峰值间距与缺陷长度存在正比例的关系。结合仿真数据得到缺陷长度L与径向磁通分量峰值间距x1的量化模型为
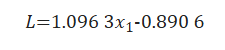
由式(6)可知,缺陷长度L与径向磁通分量峰值间距x1之间近似为线性关系,通过式(6)可量化缺陷长度。
缺陷长度固定为4 mm,缺陷深度分别设置为模拟管道试件厚度的12.5%,25%,37.5%,50%,62.5%,80%(缺陷编号分别为1,2,3,4,5,6),求解得到不同缺陷深度的漏磁信号曲线如图4所示。
由图4可知,在相同励磁条件与相同提离值的情况下,缺陷长度固定,随着缺陷深度的增加,轴向磁通分量的幅值变大,因此轴向磁通分量峰值与缺陷深度之间呈正比例关系;径向磁通分量的波形峰值变大,但变化不明显且较为缓慢,难以判断该变化与缺陷尺寸之间的联系,经过对比得出轴向磁通分量的变化特征较明显,结合仿真数据得到缺陷深度D与轴向磁通分量峰值x2的量化模型为
| <math xmlns="http://www.w3.org/1998/Math/MathML"> | (7) |
由式(7)可知,缺陷深度D与轴向磁通分量峰值x2之间呈线性关系,通过式(7)可量化缺陷深度。
为研究不同缺陷截面形状对漏磁信号的影响,对不同截面形状的缺陷进行仿真分析,在相同的励磁条件下,缺陷长度固定为4 mm,缺陷深度固定为50%试件厚度,以缺陷二维边缘轮廓面积为变化参数,分别设置为4.0,5.6,7.2,8.0,9.6,11.2 mm2(缺陷编号分别为1,2,3,4,5,6),具体缺陷截面形状如图5所示。模拟求解得到不同二维边缘轮廓面积缺陷的漏磁信号曲线如图6所示。
由图6可知,当缺陷长度与深度固定时,随着缺陷二维边缘轮廓面积的增大,轴向磁通分量的峰值不断增大,轴向磁通分量峰值与缺陷轮廓面积之间存在正比例的关系;径向磁通分量的幅值会随之增大,且径向磁通分量的峰峰值间距也缓慢增大,但增速较为缓慢,因此径向磁通分量难以表征缺陷轮廓面积信号的变化规律,结合仿真数据得到缺陷二维边缘轮廓面积S与轴向磁通分量峰值x2的量化模型为
由式(8)可知,缺陷二维边缘轮廓面积S与轴向磁通分量峰值x2之间的数学模型为线性关系模型,通过式(8)可大致估算和量化缺陷二维边缘轮廓面积。
通过上述分析可知,轴向磁通分量峰值不仅受缺陷长度和缺陷深度的影响,在同样励磁条件下,缺陷长度与深度尺寸固定时,轴向磁通分量峰值还会随着缺陷二维边缘轮廓面积的增大而增大,如果只从漏磁信号强度判断缺陷的长度与深度,会产生较明显的误差,故还应该考虑缺陷轮廓面积参数的综合影响。
试验平台结构示意及实物如图7所示。直流电源连接励磁线圈并施加5 A的直流电流为励磁源,励磁线圈匝数为450匝,铁芯材料为DT4,钢板材料为Q235,钢板尺寸(长×宽×高)为257 mm×100 mm×4 mm,钢板上缺陷长度为4 mm,缺陷深度为2 mm,缺陷二维边缘轮廓面积分别为4.0,5.6,7.2,8.0,9.6,11.2 mm2(缺陷编号为1,2,3,4,5,6),传感器位于磁芯下方且与含缺陷钢板保持1 mm提离,通过电控箱控制移动平台以0.5 cm/s的速度进行匀速移动,漏磁信号数据通过传感器传输到计算机上,经过处理后漏磁信号数据被转换为波形曲线。试验测得的波形如图8所示,可见,励磁后信号特征均与仿真结果相似。
由图8可知,不同二维边缘轮廓面积的缺陷试验结果与仿真结果基本一致,对比图6(a)与图8可以发现,随着缺陷二维边缘轮廓面积的增大,轴向磁通分量的峰值不断增大,且当缺陷二维边缘轮廓面积大于8 mm2时,轴向漏磁信号波形会出现双波峰。利用前文所述二维边缘轮廓面积缺陷量化模型,对缺陷进行量化和误差分析,结果如表1所示。试验得到的曲线信号幅值与仿真得到的曲线信号幅值基本一致,且出现了同样的波形特征,因此通过此试验平台可实现不同尺寸缺陷的检测。
| 实际面积/mm2 | 轴向分量峰值/(×10-3 T) | 计算面积/mm2 | 误差/% |
|---|---|---|---|
| 4.0 | 28.888 | 4.262 7 | 6.57 |
| 5.6 | 32.683 | 5.719 9 | 2.14 |
| 7.2 | 35.593 | 6.837 4 | -5.04 |
| 8.0 | 37.150 | 7.435 3 | -7.06 |
| 9.6 | 41.564 | 9.130 3 | -4.89 |
| 11.2 | 45.934 | 10.808 3 | -3.49 |
对不同参数的缺陷构建有限元仿真模型,得到缺陷的漏磁场信号,将最小二乘拟合曲线运用到漏磁检测缺陷识别中,获得了缺陷长度与漏磁场径向峰值间距之间的线性数学关系,缺陷深度以及缺陷轮廓面积与漏磁场轴向峰值的线性数学关系,试验结果与仿真结果基本一致。文章可为管道缺陷轮廓量化、管道损伤程度判断等提供参考,也可为工程上基于漏磁信号的管道缺陷严重程度的初步判断提供依据。
推荐阅读: